


| bidouillages mathématiques 
alphabet phonétique (étendu) | 
notation en style de fitch pour katex | 
bac-à-sable de logique polyvalente | 
autres | 
unicode
| |
les espaces Lp mesurent à quel point une fonction est "proche" d'être intégrable (principalement reportatif)
28 avril 2023l'intégrabilité est généralement assez proche d'la sommabilité. en effet, avec l'intégration d'riemann, on peut borner des fonctions positives inférieurement et supérieurement par des fonctions en escaliers/rectangulaires, avec des largeurs à jamais décroissantes jusqu'à des épaisseurs nulles, un peu comme ça :
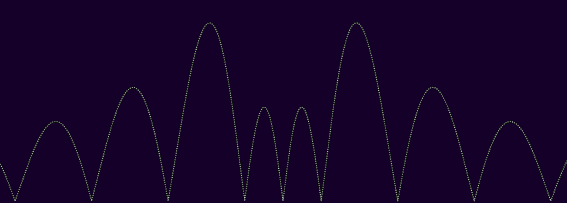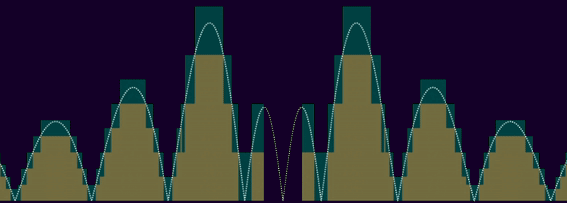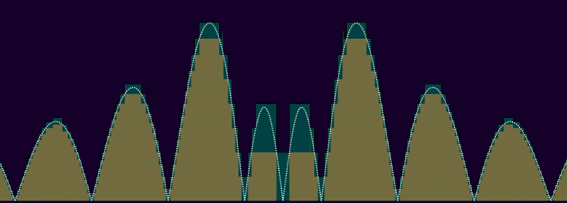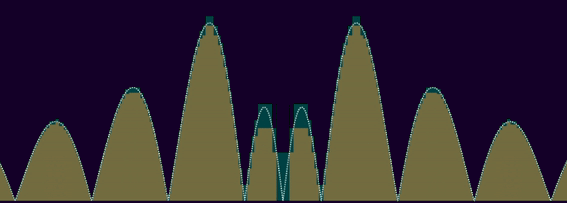
si on peut borner une fonction f avec une seule marche (ou, d'façon équivalente, un nombre fini de marches), comme avec ε·1[-n, n] (qui est ε sur [-n, n], 0 ailleurs) pour certains ε > 0 et n ≥ 0, alors l'intégrale de f sur ℝ est bornée supérieurement par l'intégrale de ε·1[-n, n], qui est 2εn < ∞ ; on appelle ce genre de fonctions des fonctions à la fois "bornées" (borne verticale) et "prise en charge de manière compacte" (borne horizontale). enfin, ça c'est selon la mesure de lebesgue, pck avec une autre peut qd mm y avoir des intégrales infinies : avec la mesure de comptage, toute f à support compact et borné tel que |f -1(ℝ\{0})| = ∞ est pas intégrable, ç'qui est pourtant une propriété commune à pratiquement toutes les fonctions usuelles sur ℝ.
la mesure habituelle λ1 (lebesgue), heureusement, a cependant la propriété qu'toute fonction bornée à support compact est d'intégrale finie. elles forment les fonctions les "plus" intégrables qui soient, mais elles sont évidemment pas seules. notamment, pour ε > 0, voici quelques exemples :
- x ⟼ 1/x1+ε est intégrable sur [1, +∞),
- x ⟼ 1/(x log1+ε(x)) sur [e, +∞),
- x ⟼ 1/(x log(x) log(log(x))1+ε) sur [ee, +∞),
- x ⟼ 1/(x log(x) log(log(x)) log(log(log(x)))1+ε) sur [eee, +∞),
- en gros, x ⟼ 1/(x log(x) log(log(x)) ··· log○n(x)1+ε) sur [e↑↑n, +∞), peu importe n ≥ 1.
en effet, on remarque que, si on note Ʒ l'ensemble des fonctions intégrables de U ⊊ ℝ dans ℝ, disons, sans perte de généralité, Ʒ ⊂ ℝℝ\{0}, que Ʒc = ℝℝ\{0}\Ʒ les non-intégrables, on a que cl(Ʒ) ⊈ Ʒ, à cause de toutes fonctions non-intégrables dans l'adhérence de Ʒ ci-haut. ainsi, Ʒ n'est pas fermé, et Ʒc n'est pas ouvert. pour oblitérer tous vos espoirs, on peut prendre une suite toute simple de fonctions non-intégrables qui tendent vers une fonction intégrable : prenons f définie presque partout et non-intégrable, (f/n)n ≥ 0 tend vers 0 presque partout, qui est intégrable. du coup, Ʒ et Ʒc sont ni ouverts ni fermés. de plus, on peut montrer que cl(Ʒ) = cl(Ʒc) = ℝℝ\{0}, car en prenant f0 non-intégrable et f1 intégrable, on a (f1 + f0/n)n ≥ 0 suite à valeurs dans Ʒc en tendant vers f1, et (1[-n,n]·min{f0,n})n ≥ 0 à valeurs dans Ʒ mais tendant vers f0. du coup, pour toute fonction f ∈ ℝℝ\{0}, on a d(f,Ʒ) = d(f,Ʒc) = 0 en ce sens... mouais, pas terrible. c'est pour ça qu'on va utiliser les normes Lp à la place.
pour f : U ⊆ ℝm ⟶ ℝn, la norme Lp est définie sur une valeur mesurable U ⊆ ℝm comme (∫U |f(x)|pdµ(x))1/p, avec µ étant généralement la mesure d'lebesgue λm sur ℝm, et |·| étant une norme sur ℝn (elles sont toutes équivalentes). en d'autres termes, être Lp évalue si |f(x)|p est intégrable, au sens le plus usuel possible. quand |f| est bornée sur un ensemble mesurable V ⊆ U, alors f est Lp(V,𝔅V, λm) si l'une d'ces deux possibilités est satisfaite : soit V est bornée, soit |f(x)| = O(ɕk,ε(x)) pour certains k ≥ 1 et ε > 0 comme |x| → ∞ (attention : c'est suffisant, mais pas nécessaire !). qd |f| est pas bornée sur V' un sous-ensemble compact de U, puisque ɕk,ε est strictement décroissante et positive sur [e↑↑k, +∞), on peut inverser ɕk,ε et on a une formule exacte pour passer d'une intégrale à l'autre comme suit :
du coup, plus p est grand, pour une fonction f ∈ Lp, plus |f| peut être étalée horizontalement, en tendant de plus en plus lentement vers 0 en ±∞, là où par contre, |f| doit avoir des asymptotes verticales de plus en plus serrées, se rapprochant géométriquement de demi-droites. voici une visualisation, où p va de 1 à 5 :
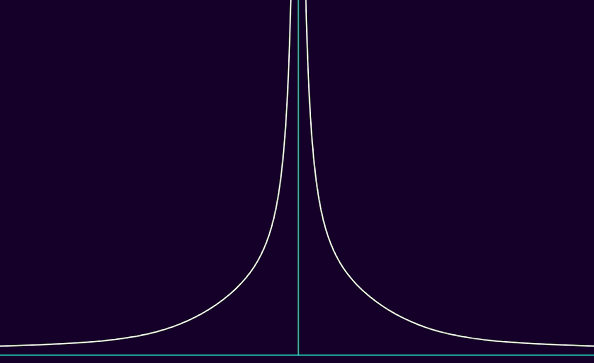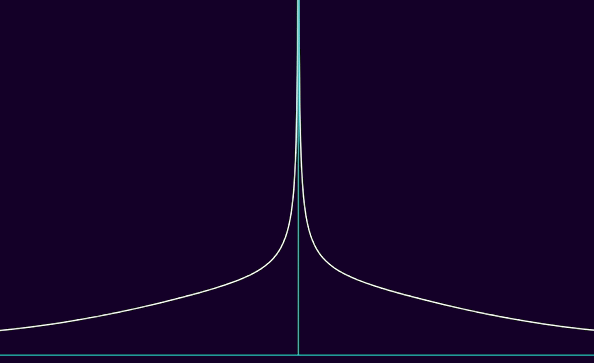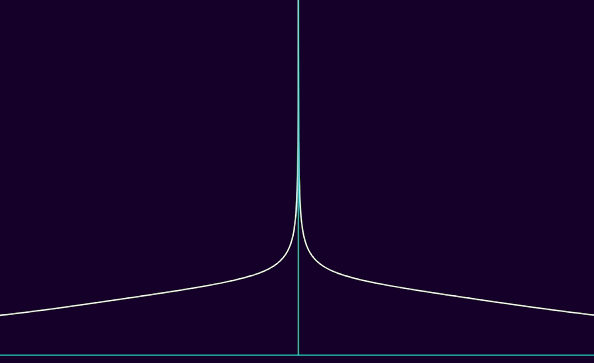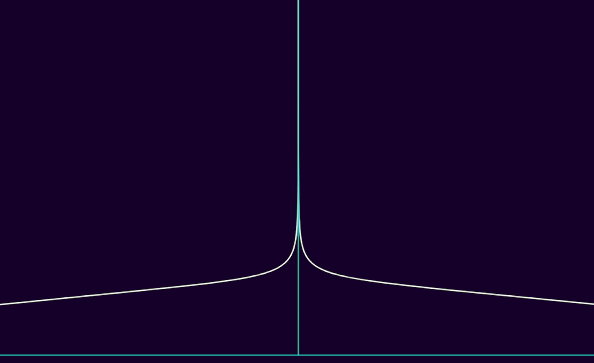
on pourrait arguer qu'cette asymétrie est un peu cheloue, et on aurait raison. on veut en gros dire qu'une fonction est d'"plus en plus intégrable" qd la fonction est Lp sur des ensembles bornés pour des valeurs de p plus grandes, mais Lq sur des ensembles non-bornés avec des valeurs de q plus petites. cependant, on veut que p et q soient liées par une certaine relation. une telle relation possible, telle que plus p est grand, plus q est petit, et 1 ≤ p, q ≤ ∞, est notamment 1/p + 1/q = 1. quand cette même relation est satisfaite, on a même un nom pour ça : on dit que p est conjugué à q, et vice-versa. si cette relation a un nom à elle seule, c'est pck c'est d'une grande importance en analyse fonctionnelle : l'espace "dual" de Lp, entre guillemets pck c'est avec des fonctions linéaires et continues plutôt qu'juste linéaire, c'est Lq qd p est conjuguée à q et vice-versa. l'inégalité de hölder dit même que, pour tout f ∈ Lp et g ∈ Lq, ||fg||L1 ≤ ||f||Lp·||g||Lq, donc avec quelques trucs de normes d'opérateur on retrouve des propriétés assez lipschitziennes grâce à cette inégalité, et lipschitzien + linéaire ⇒ continu même en dimension infinie donc c'est giga basé lol.
tl;dr. on peut dire que f est "plus" intégrable pour des valeurs grandes de p ≥ 1, si f est Lp sur des ensembles bornés, et Lq sur des ensembles non-bornés, où q = ∞ si p = 1, et 1/p + 1/q = 1 sinon.
|
|