


| mathematical shenanigans 
(extended) phonetic alphabet | 
fitch style notation for katex | 
many-valued logic playground | 
miscellaneous | 
unicode
| |
Lp spaces measure "how close" to being integrable a function is (mostly reportative)
april 28th, 2023integrability is usually quite close to summability. indeed, according to riemann integration, positive functions can be bounded by below and above by step/rectangular functions, with everdecreasing widths that tend to naught, a bit like so :
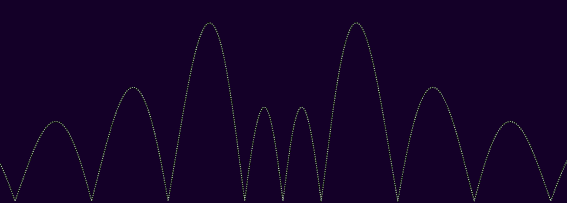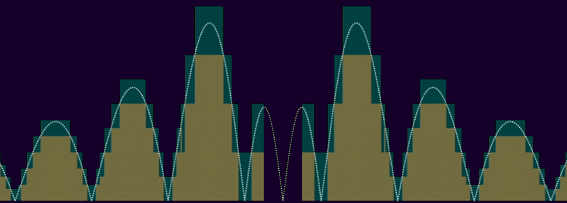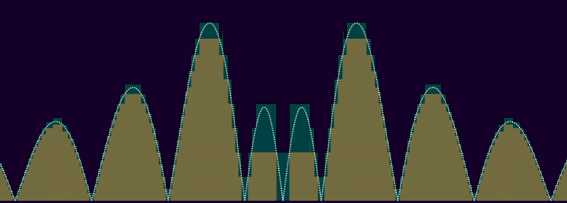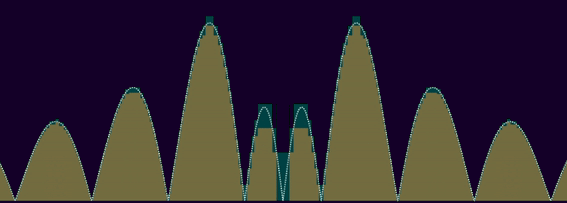
if we can bound a function f by above with a single step (or, equivalently, finitely many steps), like ε·1[-n, n] (which is ε on [-n, n], 0 elsewhere) for some ε > 0 and n ≥ 0, then the integral of f over ℝ is bounded by above by the integral of ε·1[-n, n], which is 2εn < ∞ ; we say such functions are both "bounded" (vertical bound) and "compactly supported" (horizontal bound). well, according to the lebesgue measure anyway, otherwise it can still yield infinite integrals : with the counting measure, any bounded compactly supported f such that |f -1(ℝ\{0})| = ∞ is not integrable, which is the case of most usual functions over ℝ.
the usual (lebesgue) measure λ1, thankfully, does have the property that all bounded compactly supported functions have finite integrals. these are the most integrable functions one could think of, but they're obviously not the only ones. notably, for all ε > 0, here are a few examples :
- x ⟼ 1/x1+ε is integrable over [1, +∞),
- x ⟼ 1/(x log1+ε(x)) over [e, +∞),
- x ⟼ 1/(x log(x) log(log(x))1+ε) over [ee, +∞),
- x ⟼ 1/(x log(x) log(log(x)) log(log(log(x)))1+ε) over [eee, +∞),
- basically x ⟼ 1/(x log(x) log(log(x)) ··· log○k(x)1+ε) over [e↑↑k, +∞), regardless of k ≥ 1.
(we'll call these functions ɕk,ε for each k ≥ 1, standing for the way i call them : the "cauchy border functions" (ɕ looking like "c" and "∂" merged together) to the set of non-integrable functions, while always being integrable themselves).
indeed, we can notice that, if we call Ʒ the set of integrable functions from U ⊊ ℝ to ℝ, let's say, without loss of generality, Ʒ ⊂ ℝℝ\{0}, and Ʒc = ℝℝ\{0}\Ʒ the non-integrable functions over that same set, we have that cl(Ʒ) ⊈ Ʒ, because of all the non-integrable functions in the closure of Ʒ we've shown just before. therefore, Ʒ isn't closed, and Ʒc isn't open. to obliterate all hope, there's a very simple way to generate a sequence of non-integrable functions that tend to an integrable function : take f defined over ℝ\{0}, (f/n)n ≥ 0 tends to 0 almost everywhere, which is integrable. therefore, Ʒ and Ʒc are neither open nor closed. moreover, we can even show that cl(Ʒ) = cl(Ʒc) = ℝℝ\{0}, since if we take f0 non-integrable f1 integrable, we have (f1 + f0/n)n ≥ 0 a sequence with values in Ʒc yet tends to f1, and (1[-n,n]·min{f0,n})n ≥ 0 with values in Ʒ but tends to f0. du coup, pour toute fonction f ∈ ℝℝ\{0}, we have d(f,Ʒ) = d(f,Ʒc) = 0 in that sense... just as i said, not very satisfying. that's why we'll use Lp norms instead.
for f : U ⊆ ℝm ⟶ ℝn, the Lp norm is defined over a measurable U ⊆ ℝm as (∫U |f(x)|pdµ(x))1/p, with µ usually being the lebesgue measure λm over ℝm, and |·| being a norm over ℝn (they're all equivalent). in other words, it evaluates whether |f(x)|p is integrable in the most usual sense possible. when |f| is bounded over a measurable set V ⊆ U, then f is Lp(V, 𝔅V, λm) if one of two possibilities are satisfied : either V is bounded, or |f(x)| = O(ɕk,ε(x)) for some k ≥ 1 and ε > 0 as |x| → ∞ (warning : this is sufficient, but not necessary !). when |f| is not bounded over V' a compact subset of U, since ɕk,ε is strictly decreasing and positive over [e↑↑k, +∞), we can invert ɕk,ε and we'll get an exact formula to go from one integral to the other like so :
in other words, the larger p is, for a function f to be Lp, the more |f| can spread horizontally, tending to 0 slower and slower to ±∞, whereas |f|'s vertical asymptotes have to get tighter and tighter, geometrically approaching half-lines. here's a visualisation of Lp functions, where p goes from 1 to 5 :
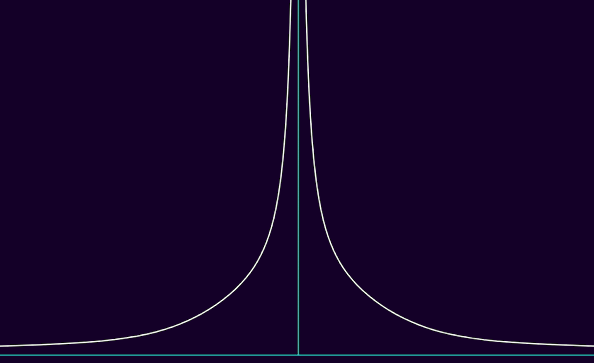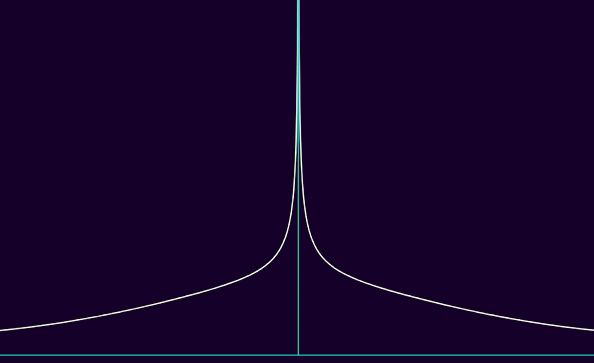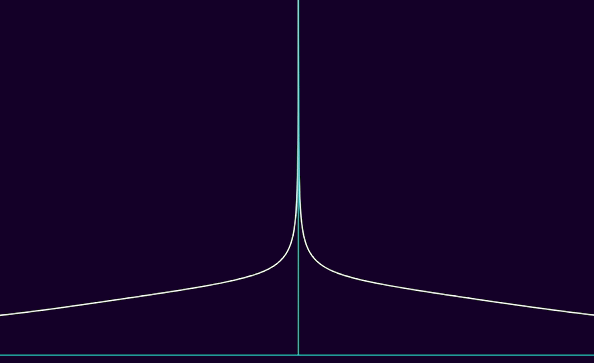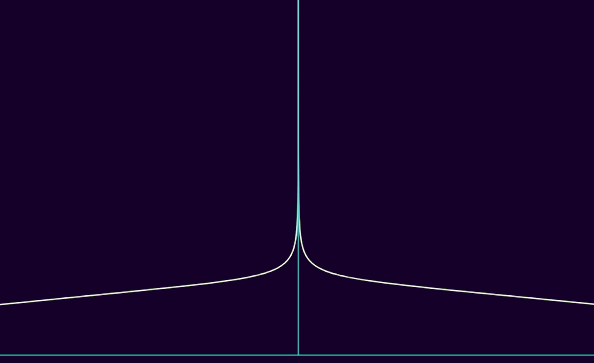
you could argue this asymmetry is quite weird, and you'd be right. we'd basically want to say that a function is more and more integrable if it's Lp over bounded sets with large enough p, and Lq over unbounded sets with smaller q. although, we'd want p and q to be linked with each other with some kind of relation. one such possible relation, where the larger p is, the smaller q is, with 1 ≤ p, q ≤ ∞, is 1/p + 1/q = 1. when this very relation is met, we actually a name for it : we say that p is conjugate to q, and vice-versa. this has a name of its own, because it's of great importance in functional analysis : the "dual" space of Lp, in terms of continuous linear functions instead of simply linear functions, is Lq, when p is conjugate to q and vice-versa. the hölder inequality also states that, for all f ∈ Lp and g ∈ Lq, ||fg||L1 ≤ ||f||Lp·||g||Lq, so with a bunch of norm operators you might get some lipschitzian shenanigans, and we know lipschitzian + linear ⇒ continuous even with infinitely many dimensions so it's pretty based ngl.
tl;dr. we could argue that f is "more" integrable for larger values of p ≥ 1, if f is Lp over bounded sets, and Lq over unbounded sets, with q = ∞ when p = 1, or 1/p + 1/q = 1 otherwise.
|
|