|
|
alexandræ.fr · distance d'objets sur des photos
distance d'objets sur des photos26 mars 2023
sur les photos, y a des angles de champ de vision (FOV, pour field of view en anglais) verticaux et horizontaux directement liés à la caméra utilisée. bien sûr, la plupart des images qu'on peut voir peuvent être recadrées, mais si on sait l'angle de la FOV (verticale ou horizontale) d'origine, et si on connait les dimensions d'origine, ça rend juste le(s) angles FOV plus petits (genre si on recadre 75% du image verticalement, ça réduit aussi l'angle du FOV vertical de 75%). dans le champ de vision vertical de la nouvelle image, l'objet prend un angle de φobjet = FOVvertical (rad)·proportion verticale de l'objet dans l'image (%).
l'objet le plus simple pour calculer la distance est une boule. si on note son rayon réel r ([longueur] en analyse dimensionnelle), puisqu'y prend un angle φboule, ça fait qu'les deux tangentes qui se croisent au point focal (la caméra) forment un angle φboule. à partir d'ces seules conditions, on peut déduire qu'la distance entre la caméra et la boule est (1/|sin(φboule/2)| − 1)R :

c'est vraiment pour des trucs plus linéaires qu'ça s'complique mdr. le premier scénario qu'j'ai compris assez facilement était quand vous avez une sorte de poteau directement tangent à une boule autour d'la caméra, où c'est assez trivialement (hauteurpoteau /2)/|tan(φpôle/2)|, où hauteurpôle est en unité d'longueur, du point d'vue d'l'analyse dimensionnelle.
cependant, c'est beaucoup plus difficile lorsque l'angle du poteau est pas exactement aussi simple (inutile de dire, la plupart du temps quoi lol). heureusement, j'ai réussi à faire tout l'boulot, mais pour la conclusion va falloir introduire une tonne de variables. l'idée qu'j'avais, c'était d'trouver les angles des moitiés supérieure et inférieure des pôles, histoire que j'puisse prendre φmoitié supérieure, et φmoitié inférieure au lieu d'simplement φ (qu'j'avais déjà réduit en sa moitié à chaque fois pour mes calculs précédents, ce n'était donc que la conclusion logique de toute façon ptdr). voici la solution visuelle :
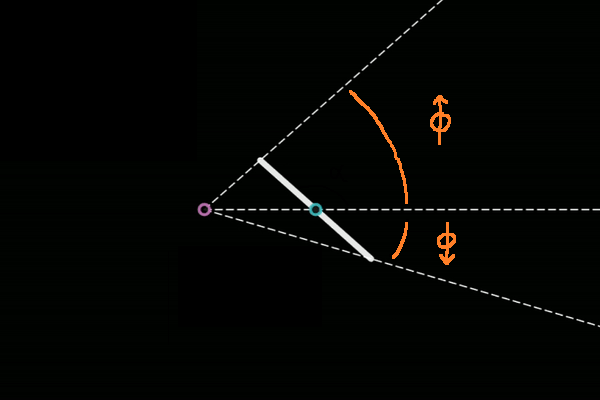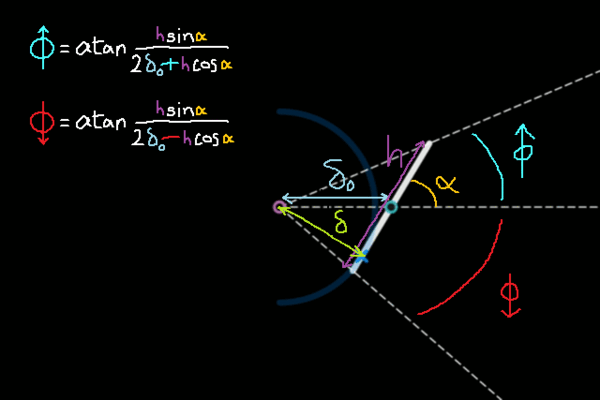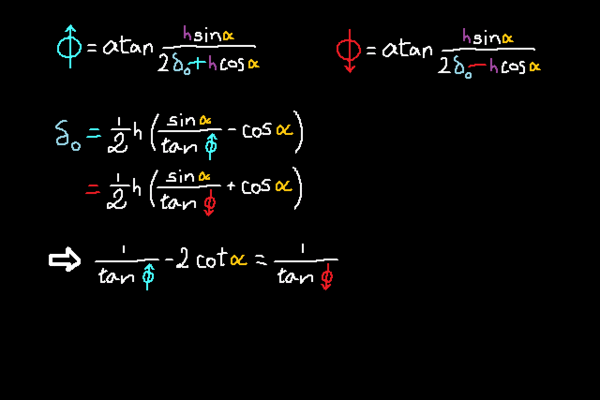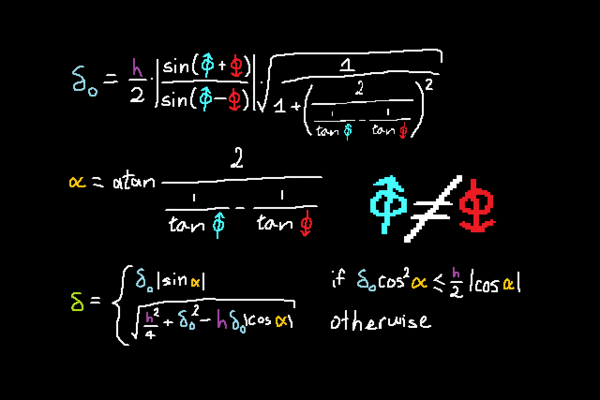
donc globalement, faut introduire deux nouvelles variables au préalable, puis après on a la distance d comme on voulait :
δ0 = · | | sin(φhaut+φbas) | | | sin(φhaut−φbas) |
· 1/2
α = atan
d =
|
|
| δ0·|sin α|
|
| si δ0·cos²α ≤ |cos α|·h/2
|
|
| √
|
| sinon
| |
bon bah voilà, on y est finalement arrivé qd mm, tant bien qu'mal ! après faites gaffe qd mm, ces calculs s'appliquent aux photos genre de caméras, ça marcherait pas avec des trucs comme les dessins pck y a pas de FOV, et y a pas des masses de courbure angulaire ; ils utilisent une autre type de perspective qui est plus linéaire en général...
| ⟨ | quelques trucs de groupes finis (su... |
| | trucs de réseaux géométriques... | ⟩ |
|
|









