|
|
alexandræ · study of an unit square-to-circle zig-zag pattern (i)
study of an unit square-to-circle zig-zag pattern (i)october 2nd, 2023
this is definitely going to be one in many entries about this pattern. during my research in analytic lattice group theory, i started studying this :
notably, i'm interested in approximating these different areas asymptotically. the reason can be found a bit in my mini-paper "fractal upper bound for Eis(R) the number of eisenstein integers of norm ≤ R".
the areas on the sides of the square are a bit peculiar, so i'll take them on their own first. we'll only need to look at an eighth of the area between the square and circle rid of its four bigger squares inscribed within that area. i will arbitrarily choose the eighth that is both vertical and adjacent to the right side. the essential function to generate every square in this specific eighth happens to be the following :
$$\begin{array}{lllll}
\textbf p&:&\mathbb R\times\mathbb R&\longrightarrow&\mathbb R\times\mathbb R\\
&&\displaystyle\binom xy&\longmapsto&\left(\begin{matrix}
\frac12\big((x+y)+\sqrt{2-(x+y)^2}\big)\\
-\sqrt{1-\frac14\big((x+y)+\sqrt{2-(x+y)^2}\big)^2}
\end{matrix}\right).
\end{array}$$
we'll have a look at two, fairly different cases, at least detail-wise. we'll proceed by generating lateral squares first, followed by all the squares adjacent to the two bigger squares that are themselves adjacent to the right and bottom sides of a given square. every square will be characterised by their bottom-right corners. here are illustrations of both scenarios, in order of mention :
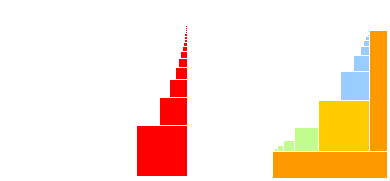
first case
the nth little square, from all the down to upwards, adjacent to the right side of the circumscriptive square has their y-axis coordinate recursively describable through \(y_{n+1}=\textbf p_y(1,y_n)\), knowing that \(y_1=-1/\sqrt2\). the thing that makes it particular is that, to study this bad boi, we gotta look at its puiseux series :
$$\textbf p_y(1,x)=-|x|\left(1+\frac x2+\underset{x\to0}o(x)\right).$$
thus, we can approximate \(y_n\) with \(z_n\) such that \(z_1:=y_1=-1/\sqrt2\), and \(z_{n+1}:=z_n+(z_n)^2/2\). it's far from a conventional recursive formula, but i had a few ideas to analyse that asymptotically. notably, since \(z_{n+1}-z_n=(z_n)^2/2\), and \(z_n\to0\), we can undiscretise the problem with the analogous differential equation \(z'(t)=z(t)^2/2\), of which we thankfully know the solutions to exhaustively be \(z:t\mapsto\displaystyle-\frac2{t+\lambda}\), where \(\lambda\) is an arbitrary real number. these are all asymptotically equivalent to \(-2/t\). due to these converging towards 0, we can say, notably thanks to the definition of derivatives, that \(z_n\sim-2/n\), and since \(y_n\sim z_n\), this means that \(y_n\sim-2/n\).
$$\begin{array}{r|ccc}
n&y_n&z_n&-\frac2{n-1+2\sqrt2}\\\hline
1&-0.70711&-0.70711&-0.70711\\
2&-0.54533&-0.45711&-0.52241\\
3&-0.44223&-0.35263&-0.41421\\
4&-0.37090&-0.29046&-0.34315\\
5&-0.31874&-0.24828&-0.29289\\
10&-0.18485&-0.14696&-0.16908\\
100&-0.02026&-0.01892&-0.01964\\
500&-0.00402&-0.00394&-0.00399\\
1\,000&-0.00201&-0.00198&-0.00200\\
5\,000&-0.00040&-0.00040&-0.00040\\
10\,000&-0.00020&-0.00020&-0.00020
\end{array}$$
second case
now, we'll assume the bottom-right corners roam more or less freely in \([1/\sqrt2,1)\times[-1/\sqrt2,0]\setminus B\big((0,0),1\big)\). for all \((x_0,y_0)\in[1/\sqrt2,1]\times[-1/\sqrt2,0]\setminus B\big((0,0),1\big)\), we define a two-sided sequence \(\left(\xi_k(x_0,y_0)\right)_{k\in\mathbb Z}\) as such :
$$\left\{\begin{array}{llll}
\xi_0(x_0,y_0)&=&(x_0,y_0)\\
\xi_{n+1}(x_0,y_0)&=&\left(x_0,\textbf p_y\!\left(\xi_n(x_0,y_0)\right)\right)&\text{if }n\ge0\\
\xi_n(x_0,y_0)&=&\left(\textbf p_x\!\left(\xi_{n+1}(x_0,y_0)\right)\!,y_0\right)&\text{if }n\lt0\\
\end{array}\right.$$
we can already see, by geometrical construction, that \(\displaystyle\lim_{n\to+\infty}\xi_n(x_0,y_0)=\left(x_0,-\sqrt{1-(x_0)^2}\right)\) and \(\displaystyle\lim_{n\to-\infty}\xi_n(x_0,y_0)=\left(\sqrt{1-(y_0)^2},y_0\right)\). contrarily to the \(x_0=1\) case, we get the following results
- when \(\frac1{\sqrt2}\le x_0\lt1\), \(\frac12\le\left.\frac\partial{\partial y}\textbf p_y\!\left(x_0,y\right)\right|_{y=-\sqrt{1-(x_0)^2}}\lt1\). the exact formula for this partial derivative is the following :
$$\partial_y:=\left.\frac\partial{\partial y}\textbf p_y\!\left(x_0,y\right)\right|_{y=-\sqrt{1-(x_0)^2}}=\frac{-x_0\sqrt{2\left(1-(x_0)^2\right)}}{\sqrt{1-2x_0\sqrt{1-(x_0)^2}}\sqrt{1-\left(x_0+\sqrt{1-(x_0)^2}\right)\sqrt{1-2x_0\sqrt{1-(x_0)^2}}}}$$
to give a sort of idea of how the function looks for \(\frac1{\sqrt2}\le x_0\lt1\), here's a fairly good approximation :
$$\left.\frac\partial{\partial y}\textbf p_y\!\left(x_0,y\right)\right|_{y=-\sqrt{1-(x_0)^2}}\approx1+\frac1{\sqrt2}x+\frac15x\left(x+\frac1{\sqrt2}\right)+\frac12x\left(x+\frac1{2\sqrt2}\right)\left(x+\frac1{\sqrt2}\right)$$
- whenever \(-\frac1{\sqrt2}\le y_0\le0\), we have \(0\le\left.\frac\partial{\partial x}\textbf p_x\!\left(x,y_0\right)\right|_{x=\sqrt{1-(y_0)^2}}\le\frac12\). i don't know any approximation that is anywhere as good as the other, so we'll have to use the exact formula computationally, which is fortunately much simpler :
$$\partial_x:=\left.\frac\partial{\partial x}\textbf p_x\!\left(x,y_0\right)\right|_{x=\sqrt{1-(y_0)^2}}=\frac12\left(1-\frac{y_0-\sqrt{1-(y_0)^2}}{\sqrt{2-\left(y_0-\sqrt{1-(y_0)^2}\right)^2}}\right)$$
this means that for all \((x_0,y_0)\), we can use the following two-sided sequence to approximate \(\left(\xi_k(x_0,y_0)\right)_{k\in\mathbb Z}\), and by "approximate", i mean asymptotic equivalence :
$$\left\{\begin{array}{llll}
\zeta_0(x_0,y_0)&=&(x_0,y_0)\\
\zeta_{n+1}(x_0,y_0)&=&\displaystyle\binom{x_0}{-\sqrt{1-(x_0)^2}}+\left(\zeta_n(x_0,y_0)-\binom{x_0}{-\sqrt{1-(x_0)^2}}\right)\left.\frac\partial{\partial y}\textbf p_y(x_0,y)\right|_{y=-\sqrt{1-(x_0)^2}}&\text{if }n\ge0\\
\zeta_n(x_0,y_0)&=&\displaystyle\binom{\sqrt{1-(y_0)^2}}{y_0}+\left(\zeta_{n+1}(x_0,y_0)-\binom{\sqrt{1-(y_0)^2}}{y_0}\right)\left.\frac\partial{\partial x}\textbf p_x(x,y_0)\right|_{x=\sqrt{1-(y_0)^2}}&\text{if }n\lt0
\end{array}\right.$$
we recognise two arithmetico-geometric sequences, and we can find a closed form for \(\left(\zeta_k(x_0,y_0)\right)_{k\in\mathbb Z}\) :
$$\left\{\begin{array}{llll}
\zeta_n(x_0,y_0)&=&\displaystyle
\binom0{x_0+\sqrt{1-(x_0)^2}}(\partial_y)^n+\binom{x_0}{-\sqrt{1-(x_0)^2}}
&\text{if }n\ge0\\
\zeta_n(x_0,y_0)&=&\displaystyle
\binom{y_0-\sqrt{1-(y_0)^2}}0(\partial_x)^n+\binom{\sqrt{1-(y_0)^2}}{y_0}
&\text{if }n\le0
\end{array}\right.$$
therefore, we have convergence with exponential decay. thus contributing much less to the overall sum of areas than first case. i'll stop here for now, i'll see what else i can come up with later !
| ⟨ | intuitionistic and paraconsistent l... |
| | which numbers to test to find a pri... | ⟩ |
|
alexandræ
|
