alexandræ français english
mathematical findings
(extended) phonetic alphabet
miscellaneous
unicode
alexandræ · density of αℕ fractional parts in [0,1] – a constructive approach

density of αℕ fractional parts in [0,1] – a constructive approach

march 20th, 2023

    when α is a rational number, αℕ can only have a fairly limited number of decimal expansions after the decimal place. for exemple, we can't converge to anything of the form n.391737636712&c within (1/3)ℕ.
    however, when α is irrational, αℕ seems to be able to approach any desired decimal expansion... but is this true? this question is quite essential, for example, to show that (ein )n≥0 defines a hilbertian basis of a particular hilbert space (wink wink fourier), as well as to understand the technique of irrational rotation found, for example, in banach-tarski's ball-doubling result. so, how to convince oneself of the well-foundedness of this observation, constructively ?

    first, here is an analogous observation on the irrationals α ∈ ]0,1[ : since (n+1)α−nα = α<1, we can get any integer as an integer part. to find such an integer, we choose m our desired integer part, and we find nα ⪎ m ⇔ n ⪎ m/α ⇐ n = ⌈m/α⌉ (⌈⌉ being the "round up"/ceiling function, unlike ⌊⌋ which is the "round down"/ceiling function, which would give the preceding integer). now, if instead we had 0.0&c, we would have exactly the same reasoning, with digits slightly shifted to the right ; in fact, we would just have to do what we just did in the previous case, although multiplied by 10. for example, for all k ∈ ℕ and d ∈ {0..9}, we have that 0.01398·⌈(10k+d)/0.1398⌋ has d as its first digit after the decimal place. by changing the base (basically the number of digits), the fact that the first digit after the decimal there is 0 in base, say, 10k, implies that the k first decimals are 0 after the comma in base 10, so if we find a way to get a 0 after the comma in any base whatsoever, solving this issue would become much more trivial.

    from the get-go, there must be at least two bgits (digits, but in base b) which are repeated infinitely often in the bcimal digits of α, otherwise we would have a repeating bgit, and therefore there would exist p ∈ ℕ such as bp(b−1)α ∈ ℕ. we can therefore write two of these bgits 1 and 2, with 1<2, such that there is an infinitely many ...12... and ...21... in the bgits. this is also not possible with bp(bq−1) for q  ∈ ℕ, so there must also be infinitely many ...11... OR ...22.. ., possibly both. if it is ...11..., then there is ...11...12... somewhere (infinitely often, in fact) in said bgits. if it's ...11..., then there's ...21...22... somewhere (infinitely often, in fact) in said bgits. it's interesting bcs that means there are two distinct positions with the same bgit (or same sequence of bgits, in fact) followed by bgits which are lower than each other, as for example in 3.141592... 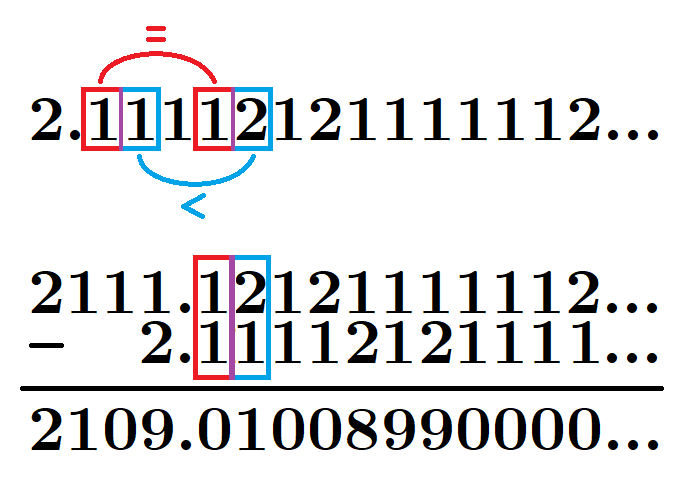where you have 1=1 and 4<5, and by explicitly noting the positions in the bgits of α so we have 3.1 14213549526..., we can get the integer 10-1(103-101) = 99, and we indeed have 99π=311.017673.... this works regardless of the base ! here is an illustration of the algorithm:


i like to summarize this algorithm with this image:


there you go, i hope y'all found it interesting!
linear interpolation, sequences, an...⟩
alexandræ
(ɔ) 2023 – 2024, intellectual property is a scam